German inflation calculator to factor inflation into any calculation

Let's say you got married in the year 2002 and had assets worth 10,000 euros. How much are these assets worth in 2025? This calculator allows you to figure out the real price of your assets based on the official consumer price index (CPI) in Germany.

When calculating your accrued gains ("Zugewinn"), you have to consider how inflation has affected the value of your assets. The initials assets, brought into the marriage on the wedding day, change value over time according to the inflation rate. The price increase is defined by the CPI difference between the starting and the ending date of the relevant period.

Content

• Inflation Calculator: Calculate price rice and inflation rate
• Calculate current monthly inflation 2025 for Germany
• Estimation of the inflation rate for coming years
• Consumer price index (CPI) for Germany
• Historical price development in Germany
• Calculation of the price rise from the consumer price index (CPI)
• Calculation of purchasing power from the consumer price index (CPI)
• How to calculate average inflation per year
• Conversion of the consumer price index (CPI) to the base year 2020

Inflation Calculator: Calculate price rice and inflation rate

The period to be considered is determined by entering the first and the last year, In each case related to the beginning and the end of the year. The smallest period to be considered is one year. If the last year entered is later than the last published year 2024, the future consumer price index (CPI) is estimated via an interpolation of the last years. The initial amount is entered for the first year. The amount output for the last year indicates by how much this initial value has increased. You can select whether the amounts are to be input or output in euros (€) or German marks (DM).

If the last year entered is the year 2025, the inflation rate and consumer index (CPI) for that year will be calculated from the current published monthly inflation rates. If the entered last year is later than the year 2025, the inflation rate for coming years is estimated.

Enter current values and select [Calculate]:

Related to the value entered in the first year, the purchasing power indicates the real value at the end of the last year. The calculated price rise is defined as the percentage change in prices between the starting and ending date of the relevant period. The average inflation rate p.a. indicates the percentage by which the prices have risen on an average per year. Last year's inflation rate indicates by how many percent prices have increased from the beginning to the end of last year.

Calculate current monthly inflation 2025 for Germany

At the end of each month, the German Federal Office of Statistics publishes the preliminary monthly inflation rate for the year 2025. The data in the following table relates to the current publication dated 2025/04/30. The annual values are the preliminary results that would result from the monthly inflation rates published to date:

Current monthly Inflation Germany 2025
Month	Inflation Rate	CPI 2024	CPI 2025
January:
February:
March:
April:
May:
June:
July:
August:
September:
October:
November:
December:
Anual Value:

The current monthly consumer price index CPI₂₀₂₅ is calculated from the monthly consumer price index CPI₂₀₂₄ of the year 2024 and the inflation rate I of the current month:

CPI₂₀₂₅ = (I / 100 + 1) * CPI₂₀₂₄.

The annual value for the consumer price index CPI 2025 is calculated from the average of the monthly values resulting from the inflation rates already published. The annual value for the CPI 2024 consumer price index is calculated from the average of the corresponding monthly values. The annual value I for the inflation rate is calculated from the two annual values of the consumer price index CPI₂₀₂₅ and CPI₂₀₂₄:

I = (CPI₂₀₂₅ / CPI₂₀₂₄ - 1) * 100.

According to this calculation, the provisional inflation rate for 2025 would be 2,2 %.

Estimation of the inflation rate for coming years

If the last year entered in the inflation calculator is later than the year 2025, the inflation rate for the coming years is estimated. For this purpose, the historical consumer price indices (CPI) of the past years are used according to the number of future years. For this past period, the average inflation rate per year and the resulting consumer price index (CPI) for the most recent year are output. In the case of estimated data, a note is displayed in the inflation calculator with the annual figures used for the estimate.

Consumer price index (CPI) for Germany

The consumer price index (CPI), published by the is a key indicator of price development in Germany. The percentage change in the CPI is referred to as an inflation rate or price increase rate. A time period with a rising price index is called inflation, a falling price index deflation. The German Excel file "consumer price index for Germany - long series from 1948" is used as the data basis for the calculations. The data used in this inflation calculator2025 refers to the current publication of 2025/04/11. Both annual values (sheet 611xx-01) and monthly values (sheet 611xx-03) are published. The results shown in this inflation calculator2025 only refer to annual values. The last published annual values therefore apply to the year 2024. For the current year 2025, a provisional consumer price index (CPI) from the average of the currently published monthly data is used. The Excel sheets contain various price indices for the cost of living for the period 1948 to 1991. Since 1991, a standardized consumer price index and an index of retail prices have also been published. To calculate the consumer price index (CPI) for the former federal territory from 1948 to 1961, the price index for the cost of living is taken from the column "4-Personenhaushalte von Arbeitern und Angestellten mit mittleren Einkommen". For 1962 to 1990 the column "Alle privaten Haushalte" is used and from 1991 the column "Verbraucherpreisindex" for Germany. The index in the published sheets refers in each case as a percentage value to a base year. For the years 1948 to 1990, the price index for the standard of living with base year 1995 (index = 100) and from 1991 the consumer price index with base year 2020 (index = 100) are published. In this inflation calculator2025 every consumer price index with the base year 1995 is converted to the base year 2020 and displayed in order to calculate the results.

Historical price development in Germany

The following charts show the historical price development in Germany. The annual values for the current year 2025 are provisional values resulting from the average of the monthly values of the inflation rates already published.

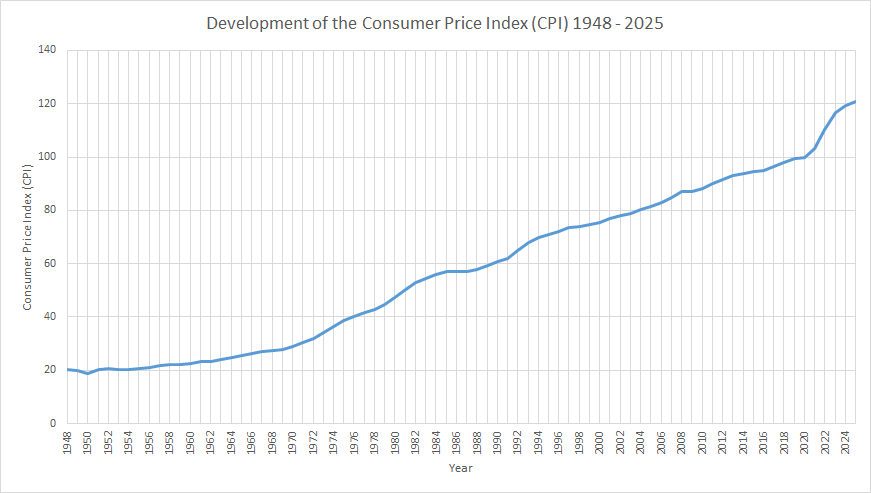
The development of the consumer price index (CPI) in Germany begins in 1948 with a value of 20.2 in relation to the base year 2020. The course of the consumer price index is a reflection of the percentage price increase over the years.

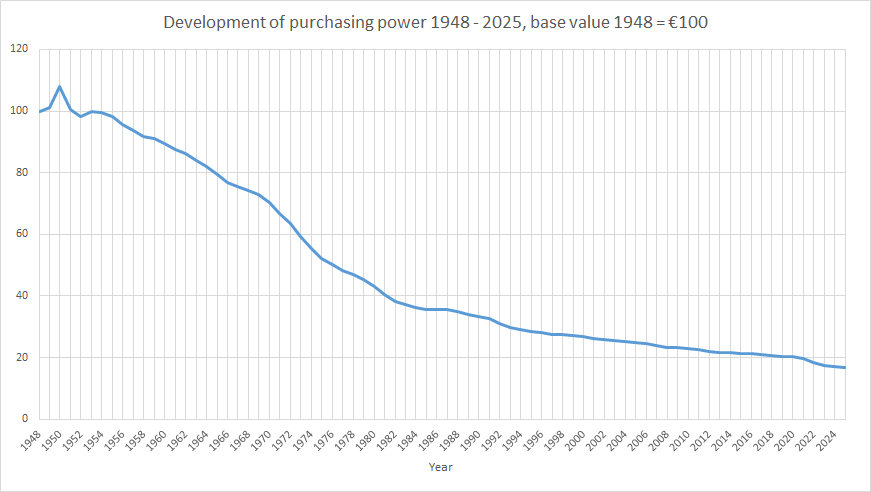
The course of purchasing power is an illustration of the loss in value of money since 1948 with a converted base value of €100. The fluctuations in price development and purchasing power are shown in more detail by the development of the inflation rate in the following diagram.

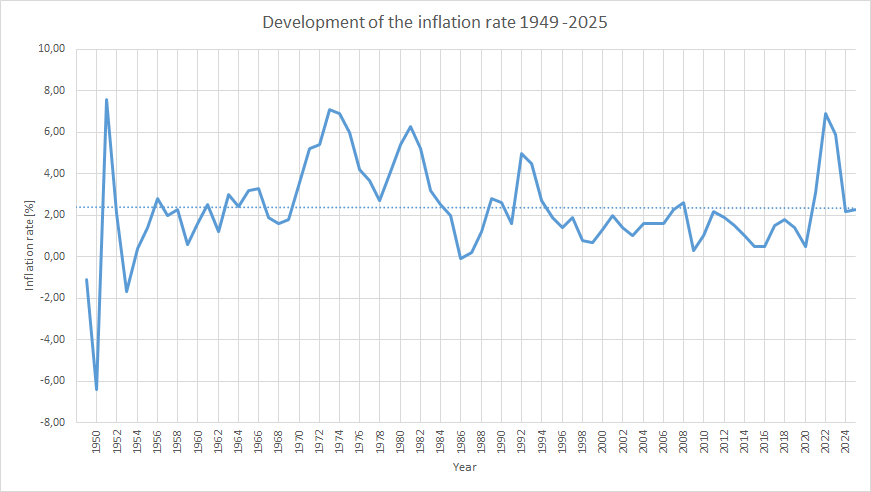
The inflation rate reflects the annual percentage increase in prices and is calculated from the annual change in the consumer price index (CPI).

The lowest inflation rate (price increase) per year over the entire period consideration started with 1948 was in the year 1950, with a negative price increase of -6.4% relative to the previous year. This means that Germany experienced a deflation, which had already begun in 1949 (-1.1%) and ended in 1950. The maximum inflation rate was in the year 1951 with a price increase of 7.6%. Germany had other years with deflation relative to the previous year in 1953 (-1.7%) and 1986 (-0.1%). High inflation rates of more than 6% relative to the previous year occurred in Germany 1973 (7.1%), 1974 (6.9%), 1981 (6.3%) and 2022 (6.9%).

Calculation of the price rise from the consumer price index (CPI)

Inflation causes prices to rise. This means that the same goods and services get a higher monetary value. The calculations are based on the annual averages of the consumer price index (CPI), which have been collected and published by German Federal Office of Statistics since 1948. The amount A₂ related to the end of the last year is calculated from the product of the amount A₁ at the end of the first year and the ratio of the consumer price index CPI₂ at the end of the last year to the consumer price index CPI₁ at the end of the first year:

A₂ = A₁ * CPI₂ / CPI₁.

For example, an amount of € 1,000 in 2018 would have a value in 2020 of:

A₂ = 1,000 * 100.0 / 96.4 = € 1,037.34.

For goods and services worth € 1000 in 2018, € 1037.34 is payable for the same goods and services in 2020. The percentage price increase P is calculated from the consumer price index CPI₂ of the last year and the consumer price index CPI₁ of the first year as follows:

P = (CPI₂ / CPI₁ - 1) * 100.

For example, a CPI of 102.0 in 2017 and a CPI of 105.8 in 2020 results in a percentage price increase P of:

P = (100.0 / 96.4 - 1) * 100 = 3.73 %.

Calculation of purchasing power from the consumer price index (CPI)

Inflation reduces the value of money, which means that money has less purchasing power. Purchasing power and price increase are reciprocal to each other. The purchasing power P related to the end of the last year is calculated from the product of the amount A at the end of the first year and the ratio of the consumer price index CPI₁ of the first year to the consumer price index CPI₂ of the last year:

P = A * CPI₁ / CPI₂.

For example, a value of € 1000 at the end of 2017 would have a purchasing power P at the end of 2020 of:

P = 1000 * 96.4 / 100.0 = € 964.00.

For € 1,000, only goods and services can be bought in 2020 that had a value of € 964.00 in 2017.

How to calculate average inflation per year

The average inflation rate spent per year applied to the amount in the first year and in each case to the resulting price increases of all subsequent years results in the amount spent in the last year. The average inflation rate per year I is calculated from the geometric mean of all consumer price indices (CPI) in the period under consideration over n years with i = 1 ... n:

x_i = CPI_i+1 / CPI_i
I = ((x₁ * x₂ * ... * x_n) ^1/n) - 1) * 100.

For the years 2017 to 2020, for example, n = 3 results in an average inflation rate I of:

x₁ = CPI₂₀₁₈ / CPI₂₀₁₇ = 98,1 / 96,4 = 1,0176
x₂ = CPI₂₀₁₉ / CPI₂₀₁₈ = 99,5 / 98,1 = 1,0143
x₃ = CPI₂₀₂₀ / CPI₂₀₁₉ = 100,0 / 99,5 = 1,0050
m = x₁ * x₂ * x₃ = 1,0373
I = (m^1/n - 1) * 100 = 1,23 %

The average inflation rate of 1.23% applied to the value of € 1,000 in the first year and to each of the following 2 years results in a price increase of € 1,037.35 in the last year:

2018: 1.23 % von € 1,000.00 = € 12.30
2019: 1.23 % von € 1,012.30 = € 12.45
2020: 1.23 % von € 1,024.75 = € 12.60

This results in a price increase of € 1,024.75 + € 12.60 = € 1,037.35. Due to rounding errors, a small deviation occurs compared to the result from the calculation of the price rise from the consumer price index (CPI).

Conversion of the consumer price index (CPI) to the base year 2020

In the published table of the Federal Statistical Office, the index for the years 1948 to 1990 is related to the base year 1995 (index = 100). In this inflation calculator 2025 all indices from this period are normalised to the currently valid reference year 2020 and displayed as the CPI:

CPI = Index₁₉₉₅ * Index_year / 100.

For the year 1948, for example, the normalized consumer price index (CPI), rounded to one decimal place, is calculated as follows:

CPI = 71.0 * 28.5 / 100 = 20.2.